Question

$ABC$ সমকোণী ত্রিভুজের $\angle B$ একটি সমকোণ, $tan A=\sqrt3$ হলে, $\sqrt3 sinA cosA=4\frac{3}{4}$ এর সত্যতা যাচাই কর।

---

নবম-দশম শ্রেণির গণিত পাঠ্য বইয়ের ত্রিকোণমিতিক অনুপাত (৯.১) এর সকল সমাধান পেতে এখানে ক্লিক করুন।

Answer 1

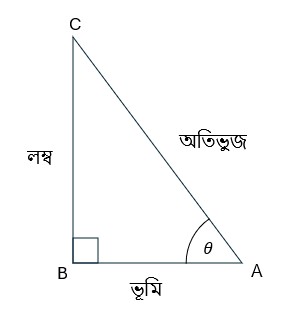
দেওয়া আছে,
$tanA=\sqrt3=$^লম্ব/_ভূমি$=\frac{BC}{AB}$$=\sqrt3=\frac{\sqrt3}{1}$

অর্থাৎ, লম্ব$=BC=\sqrt3$, ভূমি$=AB=1$, অতিভুজ$=AC=?$

আমরা জানি, পিথাগোরাসের সূত্রানুসারে,

অতিভুজ$^2$ = লম্ব$^2$ $+$ ভূমি$^2$

বা, $AC^2=BC^2+AB^2$

বা, $AC^2=\left(\sqrt3\right)^2+\left(1\right)^2$

বা, $AC^2=3+1$

বা, $AC^2=4$

বা, $AC=\sqrt4$

$\therefore$ অতিভুজ$=AC=2$

সুতরাং,

Left Hand Side,
$\sqrt3 sinA CosA$

$=\sqrt3 \cdot$ ^লম্ব/_{অতিভুজ} $\cdot$ ^ভূমি/_{অতিভুজ}

$=\sqrt3 \cdot \frac{BC}{AC} \cdot \frac{AB}{AC}$

$=\sqrt3 \cdot \frac{\sqrt3}{2} \cdot \frac{1}{2}$

$=\sqrt3 \cdot \frac{\sqrt3}{2} \cdot \frac{1}{2}$

$=\frac{\sqrt3 \times \sqrt3}{2 \times 2}$

$=\frac{3}{4}$

$=\frac{3}{4}$

সুতরাং Left Hand Side$\neq$Right Hand Side

অর্থাৎ, $\sqrt3 sinA cosA=4\frac{3}{4}$ সত্য নয়।