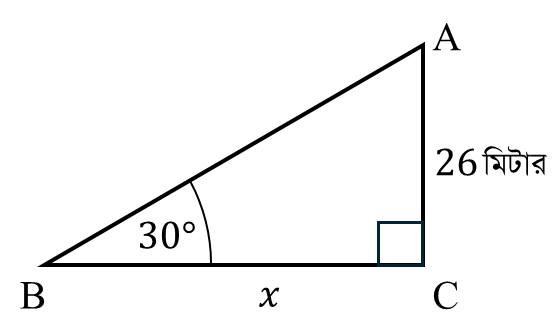
মনে করি,
মিনারের উচ্চতা $AC=26$ মিটার এবং মিনারের পাদদেশ থেকে $x$ মিটার দূরে $B$ বিন্দুতে মিনারটির শীর্ষের উন্নতি $\angle ABC=30^\circ$।
অর্থাৎ $BC=x$ মিটার।
$\triangle ABC$ থেকে পাই,
$tan \angle ABC=\frac{AC}{BC}$
বা, $tan30^\circ=\frac{26}{x}$
বা, $\frac{1}{\sqrt3}=\frac{26}{x}$
[$\because tan30^\circ=\frac{1}{\sqrt3}$]
বা, $x=26\sqrt3$
$\therefore x=45.033$ (প্রায়)
সুতরাং মিনারের পাদদেশ থেকে স্থানটির দূরত্ব $45.033$ মিটার (প্রায়) [Answer]
On QnAfy, only registered users can post questions and answers.
or use a tablet, laptop, or PC for optimal viewing.