Question

ভূতলে কোনো স্থানে একটি স্তম্ভের শীর্ষের উন্নতি $60^\circ$। ঐ স্থান থেকে $25$ মিটার পিছিয়ে গেলে স্থম্ভটির উন্নতি কোণ $30^\circ$ হয়। স্তম্ভটির উচ্চতা নির্ণয় কর।

Answer 1

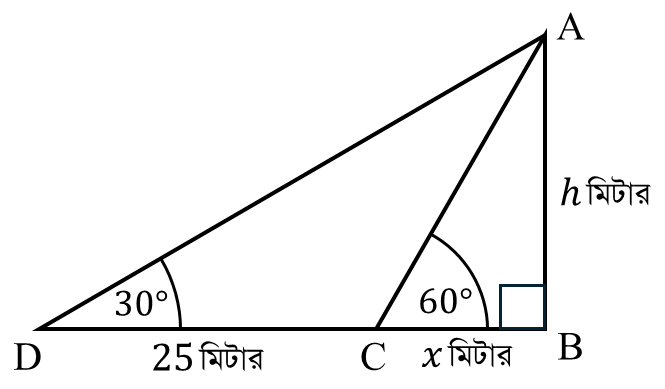
মনে করি,
স্তম্ভের উচ্চতা $AB=h$ মিটার এবং শীর্ষের উন্নতি $\angle ACB=60^\circ$। $C$ বিন্দু থেকে $CD=25$ মিটার পিছিয়ে গেলে উন্নতি $\angle ADB=30^\circ$ হয়।

ধরি, $BC=x$ মিটার

$\therefore BD=BC+CD=(x+25)$ মিটার

$\triangle ABC$ থেকে পাই,
$tan60^\circ=\frac{AB}{BC}$

বা, $\sqrt3=\frac{h}{x}$

[$\because tan60^\circ=\sqrt3$]

$\therefore x=\frac{h}{\sqrt3}$ -----($i$)

আবার, $\triangle ABD$ থেকে পাই,
$tan \angle ADB=\frac{AB}{BD}$

বা, $tan \angle30^\circ=\frac{h}{x+25}$

বা, $\frac{1}{\sqrt3}=\frac{h}{x+25}$

[$\because tan 30^\circ =\frac{1}{\sqrt3}$

বা, $\sqrt3 h=x+25$

বা, $\sqrt3h=\frac{h}{\sqrt3}+25$

[($i$) নং সমীকরণের সাহায্যে]

বা, $\sqrt3h=\frac{h+25\sqrt3}{\sqrt3}$

বা, $\sqrt3\cdot\sqrt3h=h+25\sqrt3$

বা, $3h=h+25\sqrt3$

বা, $3h-h=25\sqrt3$

বা, $2h=25\sqrt3$

বা, $h=\frac{25\sqrt3}{2}$

$\therefore h=21.651$ (প্রায়)

সুতরাং স্তম্ভটির উচ্চতা $21.651$ মিটার (প্রায়) [Answer]